Nguyễn Đăng Tiến Thành

Nguyễn Đăng Tiến Thành

I’m a Software Engineering Student at VNU-HCMUS

Sqrt decomposition and Mo’s algorithm

12 minute read

Xin chào các bạn, hôm nay mình xin được chia sẻ một chút kiến thức cũng như kinh nghiệm của mình về một phương pháp khá hay có thể sử dụng để giải các bài toán liên quan đến xử lý nhiều truy vấn trên các đoạn liên tục thuộc dãy số. Bằng cách phân chia nhỏ dãy số thành các đoạn, hay thực hiện các truy vấn theo một thứ tự nhất định thay vì thực hiện một cách không có thứ tự, nhằm tăng tốc thuật toán, đạt được hiệu quả tối đa.

Phương pháp mình nhắc tới ở đây chính là Sqrt Decomposition (chia căn) và Mo’s algorithm.

Trước khi vào nội dung, mình xin được định nghĩa trước các thuật ngữ:

  • Đoạn con (sub-array): là tập hợp các phần tử liên tiếp thuộc dãy số, ví dụ $A[l_i..r_i]$ là một đoạn con có chỉ số liên tục từ $l_i$ đến $r_i$

Hai thuật toán mình đề cập dưới đây đều có ý tưởng dựa trên một phép toán rất kì diệu trong toán học, đó là phép lấy căn, mà cụ thể ở đây là căn bậc 2. Chúng ta đều biết \(\frac{N}{\sqrt{N}} = \sqrt{N}\), bạn có thấy đó là một sự cân bằng hoàn hảo 😃.

Và bây giờ chúng ta cùng vào nội dung chính của bài viết này để hiểu tại sao nó lại kì diệu nhé. Let’s go !!!

Sqrt decomposition

Sqrt decomposition là một phương pháp cho phép thực hiện một toán tử nào đó trên đoạn con (ví dụ như lấy tổng, lấy min, max, gcd, …) trong độ phức tạp $O(\sqrt{n})$ bằng cách tiền xử lý dữ liệu (preprocessing).

Đọc đến đây thì có thể bạn sẽ thắc mắc, tại sao phải đi tính tổng các kiểu trong độ phức tạp tận $O(\sqrt{n})$ trong khi có thể sử dụng Segment tree trong độ phức tạp $O(log(n))$ hay tổng tiền tố (prefix sum) để tính tổng chỉ trong độ phức tạp $O(1)$.

Thì mình nói đến bài toán tính tổng, tìm min/max/gcd,… nhằm mục đích dễ hiểu, dễ tiếp cận, và cũng là tiền đề quan trọng để tiến đến Mo’s algorithm mình sắp đề cập ở dưới kia.

Bài toán

Cho dãy số nguyên $A$ có độ dài $N$ được đánh chỉ số bắt đầu từ $1$, và $Q$ truy vấn yêu cầu tính tổng các phần tử thuộc đoạn con $A[l_i…r_i]$.

Ý tưởng

Đầu tiên chia dãy gốc có độ dài $N$ ban đầu thành $\lceil \sqrt{N} \rceil$ đoạn (block), mỗi block có độ dài $\lceil \sqrt{N} \rceil$ bằng nhau (trừ đoạn cuối có thể ít hơn vì đôi khi $N$ không chia hết cho $\sqrt{N}$).

Đặt $s = \lceil \sqrt{N} \rceil $

Như vậy phần tử thứ $i$ của dãy sẽ thuộc vào block thứ $\lceil \frac{i}{\lceil \sqrt{N} \rceil} \rceil$

Block thứ i sẽ trải trong đoạn $[(i - 1) * s + 1, i * s]$

Giả sử với mỗi ta đã biết được tổng các phần tử trên từng block, khi gặp một truy vấn tính tổng từ $l$ đến $r$, ta có thuật toán sau

  • Xác định block mà $l$ thuộc về, gọi đó là $b_l$
  • Xác định block mà $r$ thuộc về, gọi đó là $b_r$
  • Với các block $bi$ nằm giữa $b_l$ và $br$ $(b_l < b_i < b_r)$, thay vì một vòng lặp duyệt qua tất cả các phần tử một rồi tính tổng, ta chỉ cần tính tổng của từng block.
  • Tính tổng phần còn lại bên trái và bên phải bằng vòng lặp.

Độ phức tạp

  • Tính trước tổng cho từng block tốn độ phức tạp $O(N)$
  • Tính tổng từng block nằm ở giữa, worst-case là $O(\sqrt{N})$, vì khi tính tổng các block ở giữa ta chỉ cần duyệt qua từng block và cộng thêm tổng đã tính trước trên block này. Và có tối đa $\sqrt{N}$ blocks.
  • Tính tổng phần còn lại, như đã nói mỗi block chỉ có độ dài $\sqrt{N}$, nên việc tính tổng trên block này chỉ tốn độ phức tạp $O(\sqrt{N})$

Như vậy thuật toán có độ phức tạp thời gian là $O(\sqrt{N})$, và độ phức tạp bộ nhớ là $O(\sqrt{N})$ vì phải lưu thêm mảng tổng cho từng block

Cài đặt

Tính tổng cho từng block (pre-processing)

block_size = ceil(sqrt(n));
for (int i = 1; i <= n; ++i) {
    // tương đương với ceil(i / block_size)
    int idx = (i + block_size  - 1) / block_size; 
    b[idx] += a[i]; 
}

hm… có lẽ nếu tính chỉ số từ 0 thì sẽ cài đặt dễ hơn, vì chỉ cần lấy i / block_size là được rồi.

Trả lời truy vấn

int getSum(int l, int r) {
    int sum = 0;
    int bl = (l + block_size - 1) / block_size;
    int br = (r + block_size - 1) / block_size;
    if (bl == br) { // cùng block
        for (int i = l; i <= r; ++i)
            sum += a[i];
        return sum;
    }
    // tính tổng các block ở giữa
    for (int i = bl + 1; i < br; ++i) 
        sum += b[i];
    // tính tổng phần còn lại bên trái
    for (int i = l; i <= bl * block_size; ++i) 
        sum += a[i];
    // tính tổng phần còn lại bên phải
    for (int i = br * block_size + 1; i <= r; ++i)
        sum += a[i];
    return sum;
}

hmmm… đây là cách cài đặt theo cách hiểu của mình khi chỉ mới nghe sơ qua ý tưởng thuật toán, nhìn nó khá là dài dòng, bạn có thể rút ngắn nó lại 1 vòng for là đủ :))).

OK… Vậy là ta đã xong. Có một sự thật là trước giờ mình chưa từng làm một bài nào mà dùng đến kĩ thuật này cả 😅, nên nếu có sai sót gì mong các bạn có thể giúp mình sửa chữa.

Mở rộng: các bạn hãy thử giả lại bài toán tính tổng trên bằng sqrt-decomposition nhưng có thêm thao tác cập nhật giá trị cho 1 giá trị thay vì chỉ có mỗi thao tác truy vấn tổng.

Mo’s algorithm

Okay đến cái chính mà mình muốn share hôm nay, một kĩ thuật mà mình cũng khá hay gặp trong lập trình thi đấu và mình thấy nó rất là hay khi chỉ cần dựa vào việc sắp xếp thứ tự truy vấn mà có thể tối ưu giảm độ phức tạp thời gian xuống đáng kể.

Bài toán

Ở đây mình lấy một bài toán khá là kinh điển

Cho dãy số nguyên $A$ gồm $N$ phần tử, có $Q$ truy vấn hãy cho biết có bao nhiêu số nguyên phân biệt trong đoạn $A[l_i..r_i]$

Ý tưởng

Ý tưởng mủa Mo’s algorithm cũng dựa trên việc chia dãy số thành các đoạn như sqrt-decomposition sau đó sắp xếp lại các truy vấn dựa trên cách chia đoạn này để giảm độ thức tạp tính toán.

Ở đây mình sẽ dùng một mảng $count[x]$ cho biết số $x$ đã xuất hiện bao nhiêu lần trong đoạn con đang xét. Như vậy số lượng số phân biệt trong đoạn con sẽ là số lượng giá trị $x$ thỏa mãn $count[x] > 0$. Khi thêm một phần tử giá trị $x$ vào đoạn con đang xét thì $count[x] + 1$, ngược lại khi xóa một phần tử giá trị $x$ ra khỏi đoạn con thì $count[x] - 1$.

Trước khi vào thuật chuẩn thì ta sẽ đi từ thuật đơn sơ nhất và dần dần cải tiến nó

Naive algorithm 1

Một giải thuật khá trực quan, ngây thơ để trả lời cho từng truy vấn là thực hiện một vòng lặp từ $l$ đến $r$ rồi đếm số lần xuất hiện của từng phần tử. Với mỗi truy vấn ta thực hiện độc lập.

int naive1(int l, int r) {
    int ans = 0;
    // bắt đầu mọi count[x] = 0
    for (int i = l; i <= r; ++i) {
        if (count[a[i]] == 0) {
            // nếu số a[i] chưa từng xuất hiện trước đó
            //      số lượng số phân biệt + 1
            ans++;
        }
        count[a[i]]++;
    }
    return ans;
}

Với giải thuật này, vòng lặp trong mỗi truy vấn sẽ lặp đúng $r - l + 1$ lần. Như vậy để trả lời hết cho tất cả các truy vấn sẽ có độ phức tạp bằng tổng của ($r_i - l_i + 1$ với $1 \le i \le Q$)

Naive algorithm 2

Có thật sự phải reset lại tất cả, thực hiện mỗi truy vấn độc lập? Liệu có thể tận dụng kết quả từ truy vấn trước để giải truy vấn hiện tại không?

Câu trả lời là có.

Xem hình dưới đây, ta có thể tận dụng đoạn giao nhau giữa đoạn $[l, r]$ ở truy vấn trước với đoạn $[x, y]$ của truy vấn hiện tại. Và chỉ đơn giản là mở rộng kéo r -> y và kéo l -> x, trong lúc kéo l và r về vị trí x và y ở truy vấn hiện tại, ta sẽ thực hiện cập nhật kết quả.

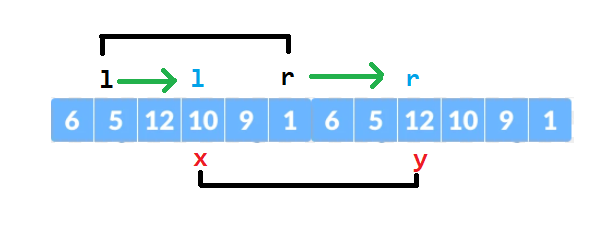
this is a placeholder image

Với ý tưởng này để thực hiện một truy vấn sẽ lặp $| r - y | + | l - x |$ lần vì ta chỉ cần duy trì hai biến $l$ và $r$ sau đó di chuyển lần lượt từng biến đến vị trí ở truy vấn hiện tại. Tại sao có dấu trị tuyệt đối? Là do ta không biết $x$ và $y$ ở truy vấn mới thật sự nằm ở đâu, nó có thể nằm hoàn toàn bên trái, hay bên phải, hay ở giữa của truy vấn trước đó.

Có thể thấy độ phức tạp cho giải thuật này là tổng $| r_i - r_{i-1} | + | l_i - l_{i - 1} |$. $(*)$

Mo’s algorithm

Okay từ hai thuật đơn sơ trên ta nhận thấy số lần lặp sẽ phụ thuộc vào thứ tự của các truy vấn (nhìn vào biểu thức $(*)$). Do đó thứ tự thực hiện truy vấn là quan trọng, và bởi vì chỉ có thao tác truy vấn kết quả chứ không có thao tác thay đổi cập nhật giá trị, nên ta hoàn toàn có thể xử lý các truy vấn offline.

Và từ nhận xét này, Mo’s algorithm đã thực hiện một thuật toán sắp xếp các truy vấn theo một thứ tự cực kì trí tuệ nhằm giảm độ phức tạp giữa các truy vấn xuống rất là hiệu quả.

Mục tiêu của thuật toán chính là giảm thiểu tổng $| r_i - r_{i-1} | + | l_i - l_{i - 1} |$. Dựa trên việc sắp xếp các đoạn trong truy vấn sau khi chia dãy gốc theo từng block độ dài $\sqrt{N}$.

Thuật toán tóm gọn như sau:

  • gọi $BLOCK = \sqrt{N}$
  • Sắp xếp các truy vấn tăng dần theo block của $l$ đó là $l/BLOCK$
  • Nếu hai truy vấn có block của $l$ bằng nhau (chung block) thì sắp xếp tăng dần theo $r$

Dùng hàm compare sau để sắp xếp các truy vấn

bool compare(const query &A, const query &B) {
    if (A.l / BLOCK != B.l / BLOCK)
        return A.l / BLOCK < B.l / BLOCK;
    return A.r < B.r;
}

Độ phức tạp

Có 2 trường hợp xả ra:

  1. Hai truy vấn chung block

    • Truy vấn $l_i$ $r_i$ chung block với truy vấn $l_{i-1}$ $r_{i - 1}$. Định nghĩa hai truy vấn chung block khi chỉ số block của $l$ bằng nhau.

    • Vì khi hai truy vấn chung block thì ta đã sắp xếp tăng dần theo $r$, nên con trỏ $r$ chỉ di chuyển tăng dần về phía bên phải, nên khi giải tất cả các truy vấn trong cùng block $l$ thì $r$ chỉ di chuyển tối đa $N$ lần nên có độ phức tạp tổng là $O(N)$

    • Còn con trỏ $l$ sẽ di chuyển chỉ trong block mà nó thuộc về, một block có độ dài $\sqrt{N}$ nên mỗi truy vấn mới $l$ sẽ di chuyển tối đa $\sqrt{N}$ lần, có tối đa $Q$ truy vấn nên độ phức tạp sẽ là $O(\sqrt{N} * Q)$

    -> Độ phức tạp: $O(\sqrt{N} * Q + N)$

  2. Hai truy vấn khác block

    • Khi từ block này sang block khác, chỉ số $r$ có thể sẽ di chuyển ở vị trí bất kì (vì điều kiện sắp xếp truy vấn) nên để chi chuyển $r$ có độ phức tạp là $O(N)$

    • Chỉ số $l$ sẽ chi chuyển tăng dần qua block khác, có tất cả $\sqrt{N}$ block nên độ phức tạp tối đa là $O(\sqrt{N})$

    Như vậy mỗi lần chuyển block sẽ có độ phức tạp $O(N)$ và có tối đa $\sqrt{N}$ lần như vậy nên độ phức tạp tổng là $O(\sqrt{N} * N)$

    -> Độ phức tạp: $O(\sqrt{N} * N)$

Độ phức tạp: $O((N + Q) * \sqrt{N})$

Ngoài ra độ phức tạp còn tùy thuộc vào hàm add hay remove

Cài đặt

Dưới đây là full code cài đặt Mo’s algorithm đã AC bài DQUERY.

#include <stdio.h>
#include <algorithm>
#include <unordered_map>

using namespace std;

const int MAXN = 3e4 + 10;
const int MAXQ = 2e5 + 10;
const int BLOCK = 175; // ~sqrt(MAXN)

struct query {
    int l, r, id;
    query(int _l = 0, int _r = 0, int _id = 0):
        l(_l), r(_r), id(_id) {};
};

int n, Q;
int a[MAXN];
int res[MAXQ];
query q[MAXQ];
int answer = 0;
unordered_map<int, int> cnt;

bool compare(const query &A, const query &B) {
    if (A.l / BLOCK != B.l / BLOCK)
        return A.l / BLOCK < B.l / BLOCK;
    return A.r < B.r;
}

void Add(int pos) {
    cnt[a[pos]]++;
    if (cnt[a[pos]] == 1) answer++;
}

void Remove(int pos) {
    cnt[a[pos]]--;
    if (cnt[a[pos]] == 0) answer--;
}

void solve() {
    int curL = 1, curR = 0;
    sort(q + 1, q + 1 + Q, compare);
    for (int i = 1; i <= Q; ++i) {
        int L = q[i].l, R = q[i].r;
        while (curL < L) Remove(curL++);
        while (curL > L) Add(--curL);
        while (curR < R) Add(++curR);
        while (curR > R) Remove(curR--);
        res[q[i].id] = answer;
    }
    for (int i = 1; i <= Q; ++i) 
        printf("%d\n", res[i]);
}

void readInput() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)
        scanf("%d", &a[i]);
    scanf("%d", &Q);
    for (int i = 1; i <= Q; ++i) {
        scanf("%d%d", &q[i].l, &q[i].r);
        q[i].id = i;
    }
}

int main() {
    readInput();
    solve();
    return 0;
}

Có thể sử dụng template hàm solve và chỉ cần thay đổi hàm Add và Remove cho phù hợp với bài toán

Luyện tập

Các bạn có thể luyện một số bài có thể dùng Mo’s algorithm để giải ở đây: Everything on Mo’s Algorithm

Tham khảo

  1. VNOI - Chia căn và ứng dụng
  2. Sqrt decomposition

You may also enjoy

System Design

2 minute read

Some little things about System Design

Hackathon Android Midterm

2 minute read

Vui viết chút về 3 ngày hackathon làm mini project giữa kì môn android