Disjoint Set Union
Giới thiệu
Disjoint Set Union (DSU) là một cấu trúc dữ liệu cho phép thực hiện thao tác kết hợp hai tập hợp bất kì lại với nhau thành một tập hợp duy nhất, và cho biết hai phần tử bất kì có thuộc cùng một tập hợp không.
Một cách thực tế, trong mạng máy tính, DSU có thể hỗ trợ nhận biết hai máy tính bất kì trong mạng có thông với nhau không, khi có thay đổi như kết nối hai mạng với nhau thông qua dây cáp.
Cấu trúc dữ liệu này đóng góp một vai trò quan trọng khi là nền tảng của một số thuật toán như Kruskal dùng để tìm cây khung ngắn nhất (Minimum Spanning Tree).
Ý tưởng
Giả sử ta đang có 3 tập hợp: [1, 3, 5], [2, 4], [7].
Quy định mỗi tập hợp sẽ có một phần tử làm gốc (phần tử được in đậm). Như vậy để biết hai phần tử có thuộc cùng một tập hợp không thì chỉ cần biết gốc của chúng có giống nhau không. Ví dụ gốc của phần tử 3 là 1, trong khi gốc của phần tử 5 cũng là 1, do đó 3 và 5 thuộc cùng một tập hợp. Khi kết hợp hai tập A và B, chỉ cần gán gốc của các phần tử trong B thành gốc của tập A là xong.
Trên là mô tả về DSU khi biểu diễn ở dạng mảng số, cũng với ý tưởng đó, người ta thường cài đặt DSU dưới cấu trúc đồ thị dạng cây. Mỗi cây sẽ thể hiện cho một tập hợp. Cài đặt DSU dưới dạng cây vô cùng ngắn gọn và hiệu quả.
Note: Để dễ hiểu, các bạn có thể vào website: visualgo.net để xem cách DSU hoạt động một cách trực quan.
Find root
Để tìm gốc (root) của một node (tương ứng với 1 phần tử). Ta cần lưu thông tin cha của node đó là ai?
Quy ước $par(root) = root$. Cha của gốc bằng chính gốc.
Như vậy tại node $x$ chỉ cần đi lên $par(x)$ cho đến khi gặp gốc là đã tìm được root :3
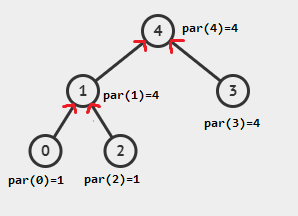
Việc từ node x tìm đến root nhanh hay chậm phụ thuộc vào việc nó ở có sâu trong cây không. Trong trường hợp suy biến, khi cây là một đường thẳng thì sẽ rất kém hiệu quả trong trường hợp cần tìm gốc nhiều lần cho các node ở sâu.
Để cải thiện hiệu năng, sau khi tìm được root ta gán luôn $par(x) \leftarrow root$ cho các node $x$ trên đường đi lên root, như vậy những lần tìm root sau của node $x$ chỉ cần nhảy lên 1 lần. Kỹ thuật này được gọi với cái tên path compression.
Union
Để hợp nhất hai cây A và B, cụ thể hơn là hợp nhất hai cây A (chứa node x) và cây B (chứa node y).
Đơn giản chỉ cần $u \leftarrow findRoot(x)$ và $v \leftarrow findRoot(y)$ sau đó gán $par(u) \leftarrow v$ (hoặc gán cha của v bằng u đều đúng - nếu chưa bàn đến độ hiệu quả).
Trường hợp $findRoot(x) = findRoot(y)$ thì hai phần tử $x$ và $y$ cùng thuộc 1 tập hợp.
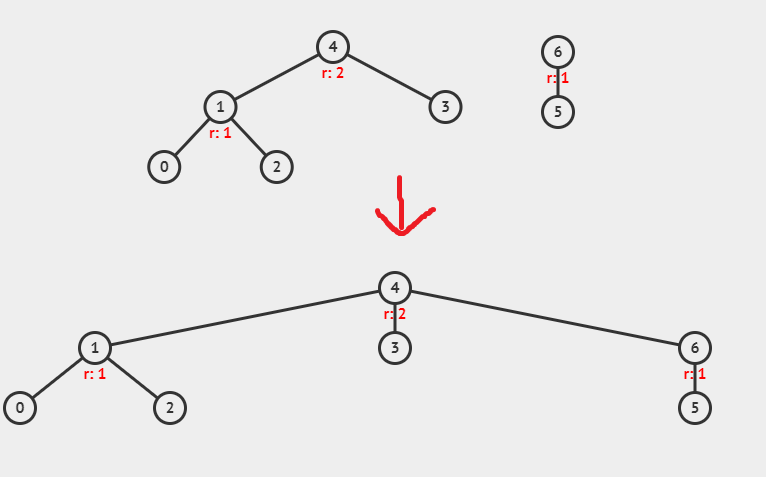
Minh họa cho union hai tập hợp [4, 1, 3, 0, 2] và [6, 5]
Có một trick để tăng hiệu năng khi union là, sử dụng union by size. Cho cây có nhiều node hơn làm gốc, trong khi cây có ít node hơn sẽ làm con.
Cài đặt
Cài đặt với path-compression
// ban đầu sẽ có n cây, mỗi cây là 1 node
void initialize(int n) {
for (int i = 1; i <= n; ++i)
par[i] = i;
}
int findRoot(int u) {
if (par[u] == u) return u; //found root
return par[u] = findRoot(par[u]); //path compressed
}
void union(int x, int y) {
par[findRoot(x)] = findRoot(y);
}
Khá ngắn gọn và trung bình đã rất nhanh O(log(n))
Cài đặt với union-by-size
Cài đặt path-compression kết hợp với union-by-size sẽ làm DSU trở nên siêu tốc độ.
Ở đây, ta cần lưu thêm thông tin $size(u)$ cho biết cây có root là $u$ chứa bao nhiêu node.
Khi union hai cây gốc $u$ và gốc $v$, nếu $size(u) > size(v)$ thì gán $par(v) = u$ ngược thì lại gán $par(u) = v$. Bên cạnh đó còn phải cập nhật lại $size$, giả sử $size(u) > size(v)$ thì cây gốc $v$ nhận cây gốc $u$ làm cha, do đó $size(u) \leftarrow size(u) + size(v)$.
Có thể tận dụng mảng $par[]$ thay cho việc dùng thêm mảng $size[]$, chỉ thay đổi một chút.
Thay vì đặt $par(root) = root$ thì ta coi $par(root) = -size(root)$, với giá trị âm này ta sẽ nhận biết được đây là root, và khi lấy $-par(root)$ đây chính là $size(root)$.
// ban đầu sẽ có n cây, mỗi cây có kích thước là 1
void initialize(int n) {
for (int i = 1; i <= n; ++i)
par[i] = -1;
}
int findRoot(int u) {
if (par[u] < 0) return u; //found root
return par[u] = findRoot(par[u]); //path compressed
}
void union(int x, int y) {
x = findRoot(x);
y = findRoot(y);
if (x == y) return; //same set
if (par[x] > par[y])
std::swap(x, y);
par[x] += par[y]; //union by size
par[y] = x;
}
Noiceee, siêu nhanh
Độ phức tạp
Khi cài đặt DSU chỉ với path compression độ phức tạp trung bình sẽ là $O(log(n))$ trên mỗi thao tác (theo trang cp-algorithm)
Khi cài DSU với path compression và union by size độ phức tạp trung bình sẽ là $O(\alpha(n))$, với $\alpha(n)$ là inverse Ackermann function, mình không rõ về hàm này lắm nhưng chỉ biết nó tăng cực chậm, chỉ khoảng 4 với $n$ lớn tầm 600 chữ số.

Kiểm nghiệm thời gian chạy thực tế bằng ngôn ngữ C++ trên bộ dữ liệu sinh ngẫu nhiên. Có thể thấy với path-compression và union-by-size DSU chạy cực nhanh, trong khi chỉ với path-compression là đã đủ nhanh rồi :3.
Luyện tập
DSU thường được sử dụng trong tìm cây khung ngắn nhất và một số dạng liên quan đến đồ thị hay tập hợp.